本文介紹Microsoft Excel中LINEST函數的語法和用法。

函數說明

LINEST函數的主要作用是使用最小二乘法對已知數據進行最佳直線擬合，并返回描述此直線的數組。因為此函數返回數值數組，所以必須以數組公式的形式輸入。

直線的公式為：

y = mx + b or

y = m1x1 + m2x2 + ... + b（如果有多個區域的 x 值）

式中，因變量 y 是自變量 x 的函數值。M 值是與每個 x 值相對應的系數，b 為常量。注意 y、x 和 m 可以是向量。LINEST 函數返回的數組為 {mn,mn-1,...,m1,b}。LINEST 函數還可返回附加回歸統計值。

函數語法

LINEST(known_y's,known_x's,const,stats)

LINEST(Y,X,邏輯值,邏輯值)

參數說明

Known_y's：是關系表達式 y = mx + b 中已知的 y 值集合。

• 如果數組 known_y's 在單獨一列中，則 known_x's 的每一列被視為一個獨立的變量。

• 如果數組 known-y's 在單獨一行中，則 known-x's 的每一行被視為一個獨立的變量。

Known_x's：是關系表達式 y = mx + b 中已知的可選 x 值集合。

• 數組 known_x's 可以包含一組或多組變量。如果只用到一個變量，只要 known_y's 和 known_x's 維數相同，它們可以是任何形狀的區域。如果用到多個變量，則 known_y's 必須為向量（即必須為一行或一列）。

• 如果省略 known_x's，則假設該數組為 {1,2,3,...}，其大小與 known_y's 相同。

Const：為一邏輯值，用于指定是否將常量 b 強制設為 0。

• 如果 const 為 TRUE 或省略，b 將按正常計算。

• 如果 const 為 FALSE，b 將被設為 0，并同時調整 m 值使 y = mx。

Stats：為一邏輯值，指定是否返回附加回歸統計值。

• 如果 stats 為 TRUE，則 LINEST 函數返回附加回歸統計值，這時返回的數組為 {mn,mn-1,...,m1,b;sen,sen-1,...,se1,seb;r2,sey;F,df;ssreg,ssresid}。

• 如果 stats 為 FALSE 或省略，LINEST 函數只返回系數 m 和常量 b。

附加回歸統計值如下：

下面的圖示顯示了附加回歸統計值返回的順序。

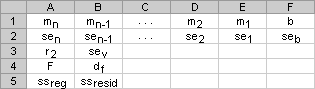
函數備注

• 可以使用斜率和 y 軸截距描述任何直線：

  斜率 (m)：
  通常記為 m，如果需要計算斜率，則選取直線上的兩點，(x1,y1) 和 (x2,y2)；斜率等于 (y2 - y1)/(x2 - x1)。

  Y 軸截距 (b)：
  通常記為 b，直線的 y 軸的截距為直線通過 y 軸時與 y 軸交點的數值。

  直線的公式為 y = mx + b。如果知道了 m 和 b 的值，將 y 或 x 的值代入公式就可計算出直線上的任意一點。還可以使用 TREND 函數。

• 當只有一個自變量 x 時，可直接利用下面公式得到斜率和 y 軸截距值：

  斜率：
  =INDEX(LINEST(known_y's,known_x's),1)

  Y 軸截距：
  =INDEX(LINEST(known_y's,known_x's),2)

• 數據的離散程度決定了 LINEST 函數計算的精確度。數據越接近線性，LINEST 模型就越精確。LINEST 函數使用最小二乘法來判定最適合數據的模型。當只有一個自變量 x 時，m 和 b 是根據下面的公式計算出的：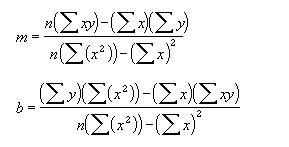

  

  其中 x 和 y 是樣本平均值，例如 x = AVERAGE(known x's) 和 y = AVERAGE(known_y's)。

• 直線和曲線函數 LINEST 和 LOGEST 可用來計算與給定數據擬合程度最高的直線或指數曲線。但需要判斷兩者中哪一個更適合數據。可以用函數 TREND(known_y's,known_x's) 來計算直線，或用函數 GROWTH(known_y's, known_x's) 來計算指數曲線。這些不帶參數 new_x's 的函數可在實際數據點上根據直線或曲線來返回 y 的數組值，然后可以將預測值與實際值進行比較。還可以用圖表方式來直觀地比較二者。

• 回歸分析時，Microsoft Excel 計算每一點的 y 的估計值和實際值的平方差。這些平方差之和稱為殘差平方和 (ssresid)。然后 Microsoft Excel 計算總平方和 (sstotal)。當 const = TRUE 或被刪除時，總平方和是 y 的實際值和平均值的平方差之和。當 const = FALSE 時，總平方和是 y 的實際值的平方和（不需要從每個 y 值中減去平均值）。回歸平方和 (ssreg) 可通過公式 ssreg = sstotal - ssresid 計算出來。殘差平方和與總平方和的比值越小，判定系數 r2 的值就越大，r2 是表示回歸分析公式的結果反映變量間關系的程度的標志。r2 等于 ssreg/sstotal。

• 在某些情況下，一個或多個 X 列可能沒有出現在其他 X 列中的預測值（假設 Y's 和 X's 位于列中）。換句話說，刪除一個或多個 X 列可能導致同樣精度的 y 預測值。在這種情況下，這些多余的 X 列應該從回歸模型中刪除。這種現象被稱為“共線”，原因是任何多余的 X 列被表示為多個非多余 X 列的和。LINEST 將檢查是否存在共線，并在識別出來之后從回歸模型中刪除任何多余的 X 列。由于包含 0 系數以及 0 se's，所以已刪除的 X 列能在 LINEST 輸出中被識別出來。如果一個或多個多余的列被刪除，則將影響 df，原因是 df 取決于被實際用于預測目的的 X 列的個數。有關計算 df 的詳細信息，請參閱下面的示例 4。如果由于刪除多余的 X 列而更改了 df，則也會影響 sey 和 F 的值。實際上，共線應該相對很少發生。但是，很可能引起共線的情況是，當某些 X 列僅包含 0's 和 1's 作為一個實驗中的對象是否屬于某個組的指示器。如果 const = TRUE 或被刪除，則 LINEST 可有效地插入所有 1's 的其他 X 列以便模型化截取。如果有一列，1 對應于每個男性的對象，0 對應于非男性對象，還有一列，1 對應于每個女性對象，0 對應于非女性對象，那么后一列就是多余的，原因是其中的項可通過從所有 1's（由 LINEST 添加）的另一列中減去“男性指示器”列中的項來獲得。

• df 的計算方法，如下所示（沒有 X 列由于共線而從模型中被刪除）：如果存在 known_x's 的 k 列和 const = TRUE 或被刪除，那么 df = n – k – 1。如果 const = FALSE，那么 df = n - k。在這兩種情況下，每次由于共線而刪除一個 X 列都會使 df 加 1。

• 對于返回結果為數組的公式，必須以數組公式的形式輸入。

• 當需要輸入一個數組常量（如 known_x's）作為參數時，以逗號作為同一行中數據的分隔符，以分號作為不同行數據的分隔符。分隔符可能因“區域設置”中或“控制面板”的“區域選項”中區域設置的不同而有所不同。

• 注意，如果 y 的回歸分析預測值超出了用來計算公式的 y 值的范圍，它們可能是無效的。?

函數示例

示例1：斜率和 Y 軸截距

注釋：示例中的公式必須以數組公式輸入。在將公式復制到一張空白工作表后，選擇以公式單元格開始的區域 A7:B7。按 F2，再按 Ctrl+Shift+Enter。如果公式不是以數組公式輸入，則返回單個結果值 2。

當以數組輸入時，將返回斜率 2 和 y 軸截距 1。

示例2：簡單線性回歸

通常，SUM({m,b}*{x,1}) 等于 mx + b，即給定 x 值的 y 的估計值。也可以使用 TREND 函數。

示例3：多重線性回歸

假設有開發商正在考慮購買商業區里的一組小型辦公樓。

開發商可以根據下列變量，采用多重線性回歸的方法來估算給定地區內的辦公樓的價值。

?

本示例假設在自變量（x1、x2、x3 和 x4）和因變量 (y) 之間存在線性關系。其中 y 是辦公樓的價值。

開發商從 1,500 個可選的辦公樓里隨機選擇了 11 個辦公樓作為樣本，得到下列數據。“半個入口”指的是運輸專用入口。

注釋：示例中的公式必須以數組公式輸入。在將公式復制到一張空白工作表后，選擇以公式單元格開始的區域 A14:E18。按 F2，再按 Ctrl+Shift+Enter。如果公式不是以數組公式輸入，則返回單個結果值 -234.2371645。

當作為數組輸入時，將返回下面的回歸統計值，可用該值可識別所需的統計值。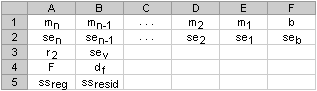

多重回歸公式，y = m1*x1 + m2*x2 + m3*x3 + m4*x4 + b，可通過第 14 行的值得到：

y = 27.64*x1 + 12,530*x2 + 2,553*x3 - 234.24*x4 + 52,318

現在，開發商用下面公式可得到辦公樓的評估價值，其中面積為 2,500 平方英尺、3 個辦公室、2 個入口，已使用 25 年：

y = 27.64*2500 + 12530*3 + 2553*2 - 234.24*25 + 52318 = $158,261

或者，可將下表復制到示例工作簿的單元格 A21。

也可以用 TREND 函數計算此值。

示例4：使用 F 和 R2 統計

在上例中，判定系數（或 r2）為 0.99675（函數 LINEST 的輸出單元格 A17 中的值），表明在自變量與銷售價格之間存在很大的相關性。可以通過 F 統計來確定具有如此高的 r2 值的結果偶然發生的可能性。

假設事實上在變量間不存在相關性，但選用 11 個辦公樓作為小樣本進行統計分析卻導致很強的相關性。術語“Alpha”表示得出這樣的相關性結論錯誤的概率。

LINEST 輸出中的 F 和 df 可被用于計算意外出現的較高 F 值的可能性。F 可與發布的 F 分布表中的值進行比較，或者 Excel 的 FDIST 可被用于計算意外出現的較高 F 值的概率。相應的 F 分布具有 v1 和 v2 自由度。如果 n 是數據點的個數，且 const = TRUE 或被刪除，那么 v1 = n – df – 1 且 v2 = df。（如果 const = FALSE，那么 v1 = n – df 且 v2 = df。）Excel 的 FDIST(F,v1,v2) 將返回意外出現的較高 F 值的概率。在示例 4 中，df = 6 (cell B18) 且 F = 459.753674 (cell A18)。

假設存在 Alpha 值等于 0.05，v1 = 11 – 6 – 1 = 4 且 v2 = 6，那么 F 的臨界值是 4.53。因為 F = 459.753674 遠大于 4.53，所以意外出現高 F 值的可能性非常低。（如果 Alpha = 0.05，假設當 F 超過臨界值 4.53 時，沒有 known_y's 和 known_x's 之間的關系可被拒絕）使用 Excel 的 FDIST 可獲得意外出現的較高 F 值的概率。FDIST(459.753674, 4, 6) = 1.37E-7，一個極小的概率。于是可以斷定，無論通過在表中查找 F 的臨界值，還是使用 Excel 的 FDIST，回歸公式都可用于預測該區域中的辦公樓的評估價值。請注意，使用在上一段中計算出的 v1 和 v2 的正確值是非常關鍵的。

示例5：計算 T 統計

另一個假設檢驗可以檢驗示例中的每個斜率系數是否可以用來估算示例 3 中的辦公樓的評估價值。例如，如果要檢驗年數系數的統計顯著水平，用 13.268（單元格 A15 里的年數系數的估算標準誤差）去除 -234.24（年數斜率系數）。下面是 T 觀察值：

t = m4 ÷ se4 = -234.24 ÷ 13.268 = -17.7

如果 t 的絕對值足夠大，那么可以斷定傾斜系數可用來估算示例 3 中的辦公樓的評估價值。下表顯示了 4 個 t 觀察值的絕對值。

如果查閱統計手冊里的表格，將會發現：雙尾、自由度為 6、Alpha = 0.05 的 t 臨界值為 2.447。該臨界值還可使用 Excel 的 TINV 函數計算，TINV(0.05,6) = 2.447。既然 t 的絕對值為 17.7，大于 2.447，則年數對于估算辦公樓的評估價值來說是一個顯著變量。用同樣方法，可以測試自變量的統計顯著水平。下面是每個自變量的 t 觀察值。

這些值的絕對值都大于 2.447；因此，回歸公式的所有變量都可用來估算區域內的辦公樓的評估價值。